R Exercises for Beginners – 11-20 – Easy Functions
1.
a. Write a function “myfun” of x to the power of its index position (x, x^2, x^3, …)
b. Test the function with an x of 1:10
#expected result [1] 1 4 27 256 3125 46656 [7] 823543 16777216 387420489 10000000000
c. Enlarge the function “myfun” with a division through the index position (x, x^2 / 2, x^3 /3, …)
#expected result [1] 1 2 9 64 625 7776 [7] 117649 2097152 43046721 1000000000
myfun = function(x){
x ^ (1 : length(x))
}b.
myfun(1:10)c.
myfun = function(x){
(x ^ (1 : length(x))/(1 : length(x)))
}
myfun(1:10) 2.
a. Write a simple moving average function (length = 3)
b. Use it on the lynx dataset
#expected result [1] 391.66667 592.33333 977.00000 1722.33333 2741.33333 4230.66667 [7] 4940.33333 4490.00000 2683.33333 1066.00000 268.33333 187.00000 [13] 290.66667 991.00000 1793.00000 2793.00000 2639.33333 1880.66667 [19] 794.66667 201.66667 88.00000 108.66667 275.66667 597.33333 [25] 1236.00000 1899.33333 1874.00000 1284.66667 565.00000 321.00000 [31] 320.66667 438.66667 909.66667 1698.00000 2411.33333 2571.66667 [37] 1891.33333 1034.00000 406.33333 260.00000 344.33333 806.66667 [43] 1828.66667 3885.00000 4762.00000 3887.33333 1732.00000 471.66667 [49] 362.00000 538.33333 912.00000 1351.33333 1840.33333 1784.33333 [55] 1477.66667 827.00000 418.66667 243.00000 299.66667 478.00000 [61] 1082.33333 1863.00000 3094.66667 3251.00000 2443.66667 991.00000 [67] 167.00000 53.66667 49.00000 98.66667 208.00000 619.00000 [73] 1900.00000 2939.33333 2704.33333 1395.66667 281.66667 215.00000 [79] 432.66667 817.33333 1843.33333 3921.00000 5589.66667 5699.33333 [85] 3981.00000 1991.66667 854.33333 511.66667 859.33333 1636.33333 [91] 2633.66667 3201.33333 3292.00000 3288.66667 2483.00000 1515.00000 [97] 278.33333 89.66667 139.00000 245.33333 586.66667 1321.00000 [103] 2379.33333 2980.33333 2682.00000 1667.00000 850.33333 558.66667 [109] 715.66667 1084.00000 1749.00000 2547.66667
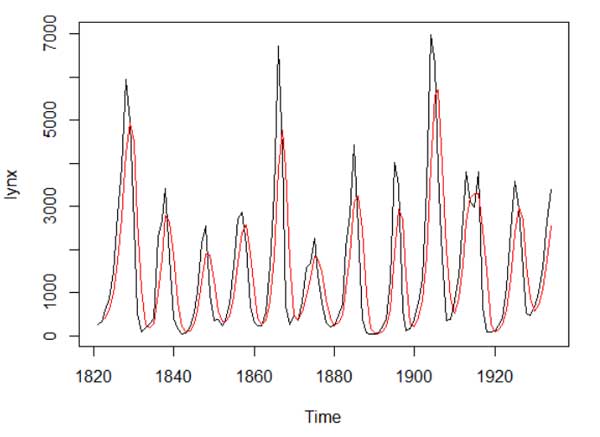
c. Plot the SMA line against the original datset in a base plot
Hint: get the SMA object in a time series class and start at the beginning of lynx+2
mySMA = function(x){
n = length(x)
(x[1:(n-2)] + x[2:(n-1)] + x[3:n] )/3
}b.
mySMA(lynx)c.
SMAline = ts(mySMA(lynx), start = 1823)
plot(lynx)
lines(SMAline, col ="red")
3.
a. Write the function “myquarter” which allocates quadrants 1:4 to the angle degrees of the vector angle. That means a value of 80° is in quadrant 1, 310 ° in quadrant 4, 400° in quadrant 1 again, and so on
b. Test the function with the values: (910, 492, 1900)
#expected result [1] 3 2 2
myquarter <- function(angle){
1 + (angle%%360)%/%90
}b.
myquarter(c(910, 492, 1900)) 4.
a. Get the matrix “mym” which consists of the 4 values 1:4
b. Double all the odd numbers in mym with a function “matrixfun”
mym = matrix(1:4, nrow = 2)b.
matrixfun <- function(mym){
mym[mym%%2 == 1] <- 2 * mym[mym%%2 == 1]
}
matrixfun(mym) 5.
Take matrix “mym” and write a function which should return a new matrix which contains all the columns without an NA in it.
mym = matrix(c(3, NA, NA, 4, 5, 6, 7, 9), nrow = 2); mym
#output
[,1] [,2] [,3] [,4]
[1,] 3 NA 5 7
[2,] NA 4 6 9
#expected result
[,1] [,2]
[1,] 5 7
[2,] 6 9
myfun <- function(mym){
mym[, !apply(is.na(mym), 2, any), drop = F]
}
myfun(mym) 6.
a. Write a function “myfun” of 2 variables, a and b, where myfun = a^b
b. Get “myfun2” which is the same as “myfun” but divided by the index position of a+1 (e.g. the first position is divided by 2, the second by 3, …)
c. Test both functions with a = 1:10 and b = 5
#myfun - expected result [1] 1 32 243 1024 3125 7776 16807 32768 59049 100000 #myfun2 - expected result [1] 0.50000 10.66667 60.75000 204.80000 520.83333 1110.85714 [7] 2100.87500 3640.88889 5904.90000 9090.90909
myfun <- function(a,b){
a^b
}b.
myfun2 <- function(a,b){
(a^b)/(2:(length(a)+1))
}c.
myfun(1:10,5)
myfun2(1:10,5) 7.
a. Write a function that generates a data.frame. Set up the function in a way so that it accepts any number of variables (hint: … as placeholder) and automatically returns the data.frame
b. Test it with those 3 vectors
a = c(3,5,6)
b = c(T,T,F)
c = c("Tom", "Ted", "Hank")
#expected result a b c 1 3 TRUE Tom 2 5 TRUE Ted 3 6 FALSE Hank
mydframe = function(...){
data = data.frame(cbind(...))
return(data)
}b.
a = c(3,5,6)
b = c(T,T,F)
c = c("Tom", "Ted", "Hank")
mydframe(a,b,c) 8.
a. Write a function “invoice” with variables pcs (nr of pieces) and unitprice the function calculates the net price (pcs * unitprice) and gives a deduction of 10% for >25 pieces sold
b. Test with 56 pieces of 89$/unit
#expected result [1] 4485.6
invoice <- function(pcs, unitprice){
net.price <- pcs * unitprice
if(pcs > 25) {
net.price <- net.price * 0.9
}
return(net.price)
}b.
invoice(pcs = 56, unitprice = 89) 9.
a. Write the function “doreturn” with variables x and y. The functions contains four steps:
a = 5*x + y b = x + 7*y r = 3*x + 9*y t = x/y - 115
Write the function in a way so that you get all four variables (a, b, r, t) returned
b. Test with 10 for x and 15 for y
#expected result [1] 65.0000 115.0000 165.0000 -114.3333
doreturn <- function(x, y) {
a = 5*x + y
b = x + 7*y
r = 3*x + 9*y
t = x/y - 115
return(c(a, b, r, t))
}b.
doreturn(10, 15)
10.
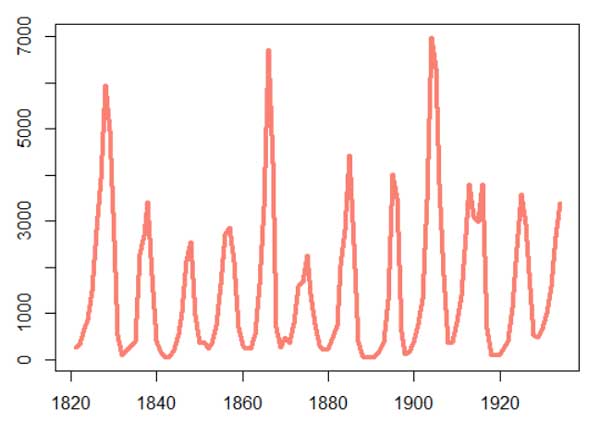
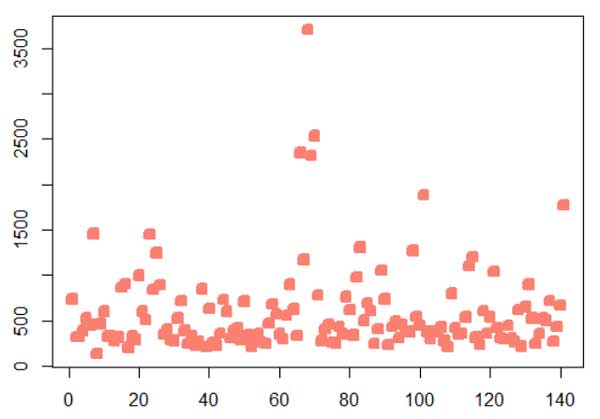
a. Write a function “myplot” which plots any data you feed into it (hint: placeholder). Preset arguments for magnification, line width, point type, color, delete lab naming
b. Test the plot function with lynx and rivers datasets
myplot <- function(...){
plot(... , pch = 12, lwd = 4,
col = "salmon",
cex = 0.9, xlab = "", ylab = "")
}b.
myplot(lynx)
myplot(rivers)



