R Exercises – 21-30 – The Apply Family of Functions
1. Function ‘apply’ on a simple matrix:
a. Get the following matrix of 5 rows and call it ‘mymatrix’
mymatrix = matrix(data = c(6,34,923,5,0, 112:116, 5,9,34,76,2, 545:549), nrow = 5)
mymatrix
[,1] [,2] [,3] [,4]
[1,] 6 112 5 545
[2,] 34 113 9 546
[3,] 923 114 34 547
[4,] 5 115 76 548
[5,] 0 116 2 549
b. Get the mean of each row
#expected result [1] 167.00 175.50 404.50 186.00 166.75
c. Get the mean of each column
#expected result [1] 193.6 114.0 25.2 547.0
d. Sort the columns in ascending order
#expected result
[,1] [,2] [,3] [,4]
[1,] 0 112 2 545
[2,] 5 113 5 546
[3,] 6 114 9 547
[4,] 34 115 34 548
[5,] 923 116 76 549
mymatrix = matrix(data = c(6,34,923,5,0, 112:116, 5,9,34,76,2, 545:549), nrow = 5)b.
apply(mymatrix, MARGIN = 1, FUN = mean)c.
apply(mymatrix, MARGIN = 2, FUN = mean)d.
apply(mymatrix, MARGIN = 2, FUN = sort)2. Using ‘lapply’ on a data.frame ‘mtcars’
a. Use three ‘apply’ family functions to get the minimum values of each column of the ‘mtcars’ dataset (hint: ‘lapply’, ‘sapply’, ‘mapply’).
Store each output in a separate object (‘l’, ‘s’, ‘m’) and get the outputs.
#expected result >l $mpg [1] 10.4 $cyl [1] 4 $disp [1] 71.1 $hp [1] 52 $drat [1] 2.76 $wt [1] 1.513 $qsec [1] 14.5 $vs [1] 0 $am [1] 0 $gear [1] 3 $carb [1] 1 >s mpg cyl disp hp drat wt qsec vs am gear carb 10.400 4.000 71.100 52.000 2.760 1.513 14.500 0.000 0.000 3.000 1.000 >m mpg cyl disp hp drat wt qsec vs am gear carb 10.400 4.000 71.100 52.000 2.760 1.513 14.500 0.000 0.000 3.000 1.000
b. Put the three outputs ‘l’, ‘s’, ‘m’ in the list ‘listobjects’
c. Use a suitable ‘apply’ function to get the class of each of the three list elements in ‘listobjects’
d. Name the output classes for each of the three functions used in the exercise
lapply(mtcars, FUN = min) -> l
sapply(mtcars, FUN = min) -> s
mapply(mtcars, FUN = min) -> m
l; s; mb.
listobjects = list(l, s, m)c.
sapply(FUN = class, X = listobjects)d.
'lapply' gives a list,
'sapply' and 'mapply' give vectors per default
3. ‘mapply’
a. Use ‘mapply’ to get a list of 10 elements. The list is an alteration of ‘A’ and ‘F’. The lengths of those 10 alternating elements decreases step by step from 10 to 1.
#expected result $A [1] "A" "A" "A" "A" "A" "A" "A" "A" "A" "A" $F [1] "F" "F" "F" "F" "F" "F" "F" "F" "F" $<NA> [1] "A" "A" "A" "A" "A" "A" "A" "A" $<NA> [1] "F" "F" "F" "F" "F" "F" "F" $<NA> [1] "A" "A" "A" "A" "A" "A" $<NA> [1] "F" "F" "F" "F" "F" $<NA> [1] "A" "A" "A" "A" $<NA> [1] "F" "F" "F" $<NA> [1] "A" "A" $<NA> [1] "F"
b. Tweak the function that you get proper element numbers (1 : 10) for the 10 list elements. Hint: argument USE.NAMES
#expected result [[1]] [1] "A" "A" "A" "A" "A" "A" "A" "A" "A" "A" [[2]] [1] "F" "F" "F" "F" "F" "F" "F" "F" "F" [[3]] [1] "A" "A" "A" "A" "A" "A" "A" "A" [[4]] [1] "F" "F" "F" "F" "F" "F" "F" [[5]] [1] "A" "A" "A" "A" "A" "A" [[6]] [1] "F" "F" "F" "F" "F" [[7]] [1] "A" "A" "A" "A" [[8]] [1] "F" "F" "F" [[9]] [1] "A" "A" [[10]] [1] "F"
mapply(rep, c("A", "F"), 10:1)b.
mapply(rep, c("A", "F"), 10:1, USE.NAMES = F)
#proper element numbers 4. Titanic Casualties – Use the standard ‘Titanic’ dataset which is part of R Base
a. Use an appropriate apply function to get the sum of males vs females aboard.
#expected result Male Female 1731 470
b. Get a table with the sum of survivors vs sex.
#expected result
Survived
Sex No Yes
Male 1364 367
Female 126 344
c. Get a table with the sum of passengers by sex vs age.
#expected result
Sex
Age Male Female
Child 64 45
Adult 1667 425
apply(Titanic, 2, sum)b.
apply(Titanic, c(2,4), sum)c.
apply(Titanic, c(3,2), sum) 5. Extracting elements from a list of matrices with ‘lapply’
a. Create ‘listobj’ which is a list of four matrices – see data:
first = matrix(38:66, 3) second = matrix(56:91, 3) third = matrix(82:145, 3) fourth = matrix(46:93, 5) listobj = list(first, second, third, fourth)
b. Extract the second column from the list of matrices (from each single matrix).
#expected result [[1]] [1] 41 42 43 [[2]] [1] 59 60 61 [[3]] [1] 85 86 87 [[4]] [1] 51 52 53 54 55
c. Extract the third row from the list of matrices.
#expected result [[1]] [1] 40 43 46 49 52 55 58 61 64 38 [[2]] [1] 58 61 64 67 70 73 76 79 82 85 88 91 [[3]] [1] 84 87 90 93 96 99 102 105 108 111 114 117 120 123 126 129 132 135 138 141 144 83 [[4]] [1] 48 53 58 63 68 73 78 83 88 93
first = matrix(38:66, 3)
second = matrix(56:91, 3)
third = matrix(82:145, 3)
fourth = matrix(46:93, 5)
listobj = list(first, second, third, fourth)b.
lapply(listobj,"[", , 2)c.
lapply(listobj,"[", 3 , ) 6. Plotting with the ‘apply’ family. Use the dataset ‘iris’ from R Base.
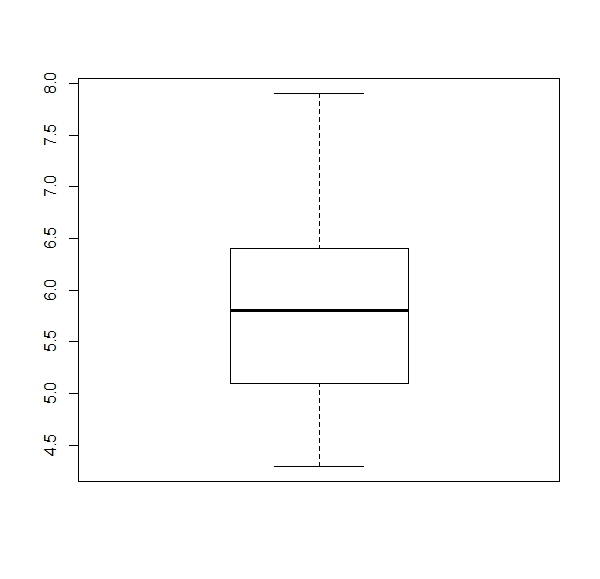
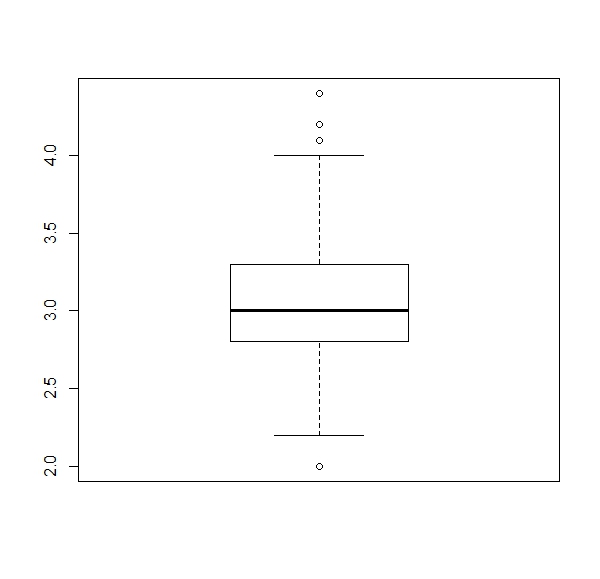
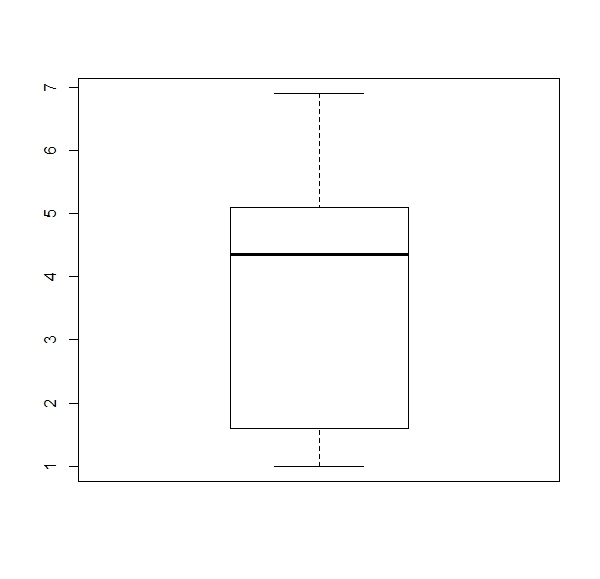
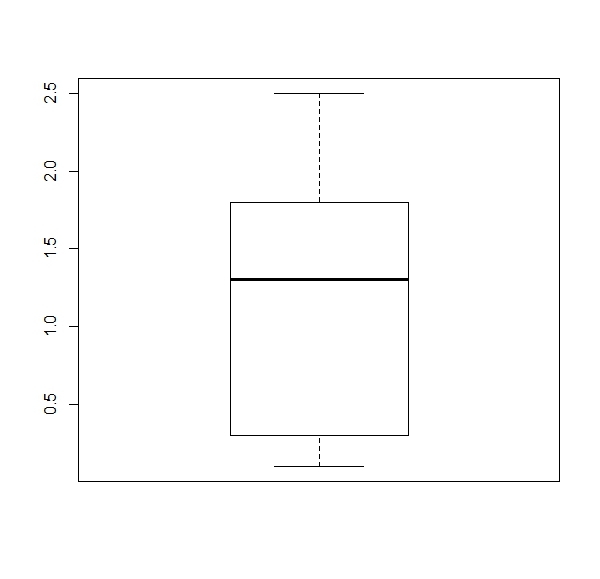
a. Get a boxplot for each numerical column of the ‘iris’ dataset (four boxplots).
Expected results:
b. The package ‘vioplot’ has a useful function ‘vioplot’ for violin plots (hint: install and activate package). Get one violin plot for each numeric column, remove any numbers from the x axis, color = salmon
Expected results:
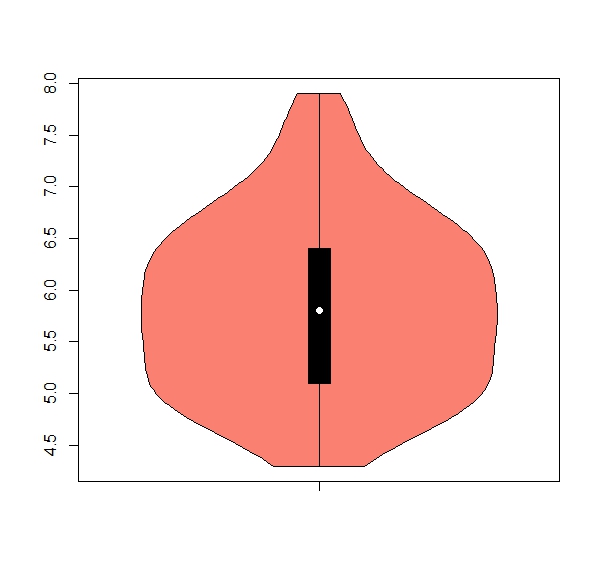
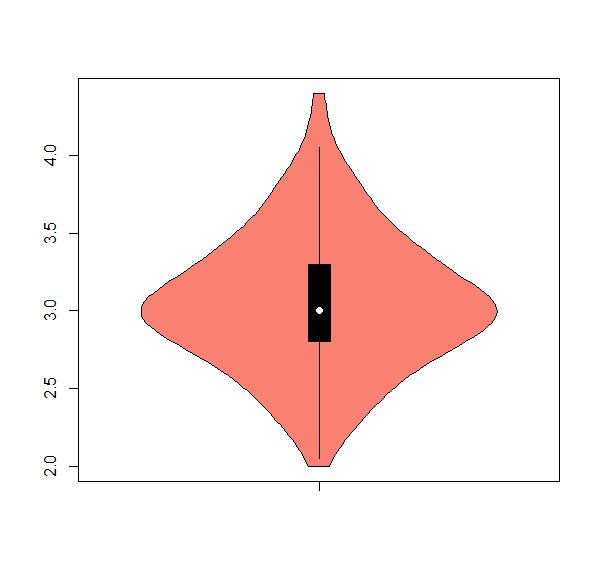
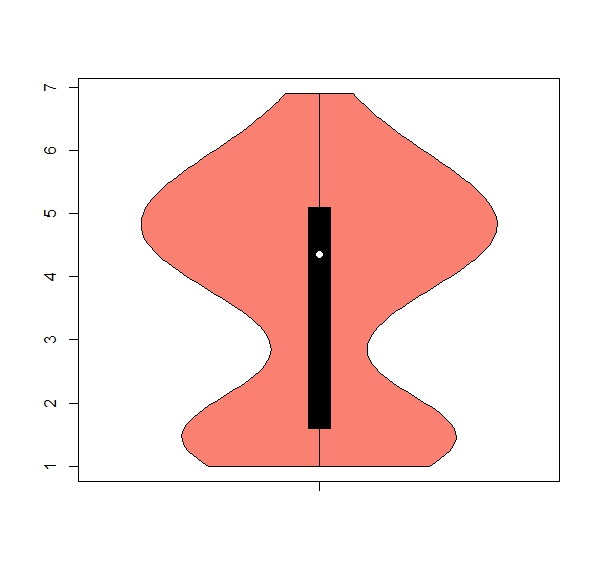
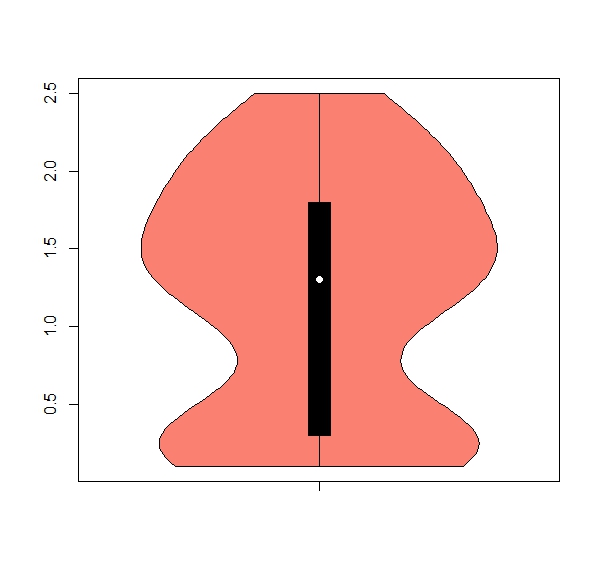
apply(iris[,1:4], 2, boxplot)b.
library(vioplot)
apply(iris[,1:4], 2, vioplot, col = "salmon", names = "") 7. Using the ‘apply’ family to work with classes of data.frames
a. Find out which column of iris is not numeric.
b. Identify the levels of the non-numeric column (hint: ‘levels’ function).
c. Try the function “unique” instead, compare the output.
which(sapply(iris, class) != "numeric")b.
levels(iris$Species)c.
unique(iris$Species)"levels" gets you character outputs which are easier to work with, "unique" gets you the original factors
8. Use library ‘ggplot2’, dataset = ‘diamonds’ (hint: install and activate package)
a. Load the library ‘ggplot2’, and dataset ‘diamonds’.
b. Which columns are not numeric in class?.
c. For observations 10000 to 11000, get the mean of columns 8, 9, 10.
d. Same as ‘c’ but round the results to one digit.
e. Sort the rounded results in ascending order.
library(ggplot2)b.
which(sapply(diamonds, class) != "numeric")c.
apply(diamonds[10000:11000, 8:10], 1, mean)d.
round(apply(diamonds[10000:11000, 8:10], 1, mean),1)e.
sort(round(apply(diamonds[10000:11000, 8:10], 1, mean),1)) 9. Function ‘aggregate’
a. Use ‘aggregate’ on ‘mtcars’. Calculate the median for each column sorted by the number of carburetors. Use the standard ‘x’, ‘by’ and ‘FUN’ arguments.
#expected result Group.1 mpg cyl disp hp drat wt qsec vs am gear carb 1 1 22.80 4 108.00 93 3.850 2.320 19.470 1.0 1 4.0 1 2 2 22.10 4 143.75 111 3.730 3.170 17.175 0.5 0 4.0 2 3 3 16.40 8 275.80 180 3.070 3.780 17.600 0.0 0 3.0 3 4 4 15.25 8 350.50 210 3.815 3.505 17.220 0.0 0 3.5 4 5 6 19.70 6 145.00 175 3.620 2.770 15.500 0.0 1 5.0 6 6 8 15.00 8 301.00 335 3.540 3.570 14.600 0.0 1 5.0 8
b. Calculate again the median based on ‘carb’, but this time use the ‘formula-dot’ notation.
#expected result carb mpg cyl disp hp drat wt qsec vs am gear 1 1 22.80 4 108.00 93 3.850 2.320 19.470 1.0 1 4.0 2 2 22.10 4 143.75 111 3.730 3.170 17.175 0.5 0 4.0 3 3 16.40 8 275.80 180 3.070 3.780 17.600 0.0 0 3.0 4 4 15.25 8 350.50 210 3.815 3.505 17.220 0.0 0 3.5 5 6 19.70 6 145.00 175 3.620 2.770 15.500 0.0 1 5.0 6 8 15.00 8 301.00 335 3.540 3.570 14.600 0.0 1 5.0
aggregate(x = mtcars, by = list(mtcars$carb), FUN = median)b.
aggregate(. ~ carb, data = mtcars, median) 10. Modulo division in a matrix
a. Get the object ‘mymatrix’ as below
mymatrix = matrix(data = c(6,34,923,5,0, 112:116, 5,9,34,76,2, 545:549), nrow = 5)
> mymatrix
[,1] [,2] [,3] [,4]
[1,] 6 112 5 545
[2,] 34 113 9 546
[3,] 923 114 34 547
[4,] 5 115 76 548
[5,] 0 116 2 549
c. Use ‘apply’ to perform a modulo division by 10 on each value of the matrix. The new matrix contains the rest of the modulo division.
#expected result
[,1] [,2] [,3] [,4]
[1,] 6 2 5 5
[2,] 4 3 9 6
[3,] 3 4 4 7
[4,] 5 5 6 8
[5,] 0 6 2 9
mymatrix = matrix(data = c(6,34,923,5,0, 112:116, 5,9,34,76,2, 545:549), nrow = 5)
mymatrixa.
apply(mymatrix, c(1,2), function(x) x%%10)